AIC - Block Prediction Implementation Details

This page describes some implementation details for the Block Prediction algorithms implemented in the Advanced Image Coding software.

Let P[x,y] be the block to be predicted, x and y ranging from 0..7.
Let S[x,y] be the source image to predict from, where S[0,0] is anchored at the current (prediction) position in the image. The source image contains the previously decoded blocks.
All positions in block P, for x, y = 0..7 are predicted according to one of the 9 prediction modes:

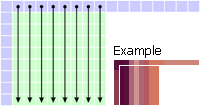Mode 0: Vertical
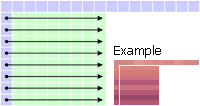The upper pixels are extrapolated vertically:

P[x,y] = S[x,-1]

Mode 1: Horizontal
The left pixels are extrapolated horizontally:

P[x,y] = S[-1,y]

Mode 2: DC
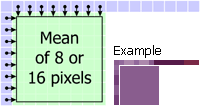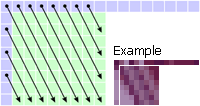
When both the upper and left samples are available, the mean of the upper and left samples is used for the entire block:

P[x,y] = (Sum(S[0..7,-1]) + Sum(S[-1,0..7]) + 8) / 16

If the upper samples are not available, only the left samples are used:

P[x,y] = (Sum(S[-1,0..7]) + 4) / 8

If the left samples are not available, only the upper samples are used:

P[x,y] = (Sum(S[0..7,-1]) + 4) / 8

If both left and upper samples are not available (first block in image), the value 128 is used (50% gray):

P[x,y] = 128

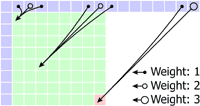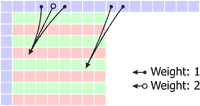
Mode 3: Diagonal Down-Left
The pixels are interpolated at a 45° angle from the upper-right to the lower-left corner.
For the bottom-right pixel (the red cell in the figure on the left), the predicted value is a weighted average of the two top rightmost pixels:

P[7,7] = (S[14,-1] + 3 * S[15,-1] + 2) / 4

For all other pixels, the predicted value is the weighted average of three successive pixels on the top row:

P[x,y] = (S[x+y,-1] + 2 * S[x+y+1,-1] + S[x+y+2,-1] + 2) / 4

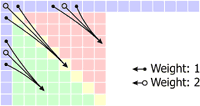Mode 4: Diagonal Down-Right
The pixels are interpolated at a 45° angle from the upper-left to the lower-right corner.
For the pixels on the down-right diagonal (x=y, the yellow cells in the figure on the left), the predicted value is the weighted average of the three top-left pixels:

P[x,y] = (S[-1,0] + 2 * S[-1,-1] + S[0,-1] + 2) / 4

For the pixels in the bottom-left triangle (x<y, the green cells), the predicted value is the weighted average of three pixels on the left column:

P[x,y] = (S[-1,y-x-2] + 2 * S[-1,y-x-1] + S[-1,y-x] + 2) / 4

For all other pixels (x>y, the red cells), the predicted value is the weighted average of three pixels on the top row:

P[x,y] = (S[x-y-2,-1] + 2 * S[x-y-1,-1] + S[x-y,-1] + 2) / 4

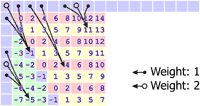Mode 5: Vertical-Right
The pixels are interpolated at a 26.6° angle from the upper-left corner to the lower edge at half the width.
First, calculate z=2*x-y. For all non-negative even values of z (the red cells in the figure on the left), the predicted value is the average of two pixels on the top row:

P[x,y] = (S[x-(y/2)-1,-1] + S[x-(y/2),-1] + 1) / 2

For positive odd values of z (the yellow cells), the predicted value is the weighted average of three pixels on the top row:

P[x,y] = (S[x-(y/2)-2,-1] + 2 * S[x-(y/2)-1,-1] + S[x-(y/2),-1] + 2) / 4

For z = -1 (the blue cells), the predicted value is the weighted average of the three top-left pixels:

P[x,y] = (S[-1,0] + 2 * S[-1,-1] + S[0,-1] + 2) / 4

For all other values of z (the green cells), the predicted value is the weighted average of three pixels on the left column:

P[x,y] = (S[-1,y-x-1] + 2 * S[-1,y-x-2] + S[-1,y-x-3] + 2) / 4

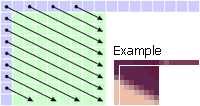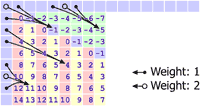Mode 6: Horizontal-Down
The pixels are interpolated at a 26.6° angle from the upper-left corner to the right edge at half the height.
First, calculate z=2*y-x. For all non-negative even values of z (the red cells in the figure on the left), the predicted value is the weighted average of two pixels on the left column:

P[x,y] = (S[-1,y-(x/2)-1] + S[-1,y-(x/2)] + 1) / 2

For positive odd values of z (the yellow cells), the predicted value is the weighted average of three pixels on the left column:

P[x,y] = (S[-1,y-(x/2)-2] + 2 * S[-1,y-(x/2)-1] + S[-1,y-(x/2)] + 2) / 4

For z = -1 (the blue cells), the predicted value is the weighted average of the three top-left pixels:

P[x,y] = (S[-1,0] + 2 * S[-1,-1] + S[0,-1] + 2) / 4

For all other values of z (the green cells), the predicted value is the weighted average of three pixels on the top row:

P[x,y] = (S[x-y-1,-1] + 2 * S[x-y-2,-1] + S[x-y-3,-1] + 2) / 4


Mode 7: Vertical-Left
The pixels are interpolated at a 26.6° angle from the upper-right corner to the lower edge at half the width.
For the odd rows (the red cells in the figure on the left), the predicted value is the weighted average of three pixels on the top row:

P[x,y] = (S[x+(y/2),-1] + 2 * S[x+(y/2)+1,-1] + S[x+(y/2)+2,-1] + 2) / 4

For the even rows (the green cells), the predicted value is the average of two pixels on the top row:

P[x,y] = (S[x+(y/2),-1] + S[x+(y/2)+1,-1] + 1) / 2

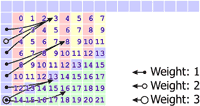Mode 8: Horizontal-Up
The pixels are interpolated at a 26.6° angle from the lower-left corner to the right edge at half the height.
The pixels in the bottom-right corner cannot be predicted from lower pixels, since these pixels have not yet been encoded/decoded yet. These pixels are set to the bottom-most available previously decoded pixel.
First, calculate z=x+2*y. For all even values of z below 13 (the red cells), the predicted value is the average of two pixels on the left column:

P[x,y] = (S[-1,y+(x/2)] + S[-1,y+(x/2)+1] + 1) / 2

For all odd values of z below 12 (the yellow cells), the predicted value is the weighted average of three pixels on the left column:

P[x,y] = (S[-1,y+(x/2)] + 2 * S[-1,y+(x/2)+1] + S[-1,y+(x/2)+2] + 2) / 4

For z=13 (the blue cells), the predicted value is the weighted average of the two left bottommost pixels:

P[x,y] = (S[-1,6] + 3 * S[-1,7] + 2) / 4

For all other values of z (the green cells), the predicted value is equal to the left bottommost pixel:

P[x,y] = S[-1,7]